Thresholding

Thresholding is used to create a binary image from a grayscale image [1].

[1]

https://en.wikipedia.org/wiki/Thresholding_%28image_processing%29

See also

A more comprehensive presentation on Thresholding

import matplotlib.pyplot as plt
from skimage import data
from skimage.filters import threshold_otsu

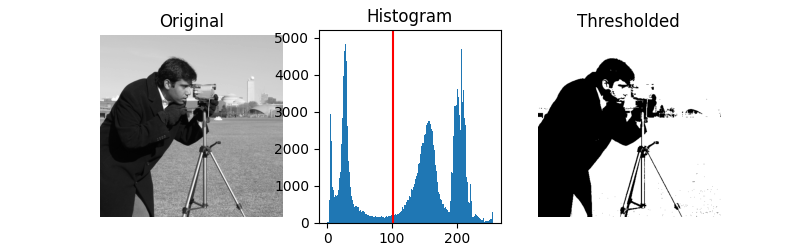
We illustrate how to apply one of these thresholding algorithms. Otsu’s method [2] calculates an “optimal” threshold (marked by a red line in the histogram below) by maximizing the variance between two classes of pixels, which are separated by the threshold. Equivalently, this threshold minimizes the intra-class variance.

[2]

https://en.wikipedia.org/wiki/Otsu’s_method

image = data.camera()
thresh = threshold_otsu(image)
binary = image > thresh

fig, axes = plt.subplots(ncols=3, figsize=(8, 2.5))
ax = axes.ravel()
ax[0] = plt.subplot(1, 3, 1)
ax[1] = plt.subplot(1, 3, 2)
ax[2] = plt.subplot(1, 3, 3, sharex=ax[0], sharey=ax[0])

ax[0].imshow(image, cmap=plt.cm.gray)
ax[0].set_title('Original')
ax[0].axis('off')

ax[1].hist(image.ravel(), bins=256)
ax[1].set_title('Histogram')
ax[1].axvline(thresh, color='r')

ax[2].imshow(binary, cmap=plt.cm.gray)
ax[2].set_title('Thresholded')
ax[2].axis('off')

plt.show()

/home/runner/work/scikit-image/scikit-image/doc/examples/segmentation/plot_thresholding.py:39: MatplotlibDeprecationWarning:

Auto-removal of overlapping axes is deprecated since 3.6 and will be removed two minor releases later; explicitly call ax.remove() as needed.

If you are not familiar with the details of the different algorithms and the underlying assumptions, it is often difficult to know which algorithm will give the best results. Therefore, Scikit-image includes a function to evaluate thresholding algorithms provided by the library. At a glance, you can select the best algorithm for your data without a deep understanding of their mechanisms.

from skimage.filters import try_all_threshold

img = data.page()

fig, ax = try_all_threshold(img, figsize=(10, 8), verbose=False)
plt.show()