Module: restoration¶
Image restoration module.
|
Create a ball kernel for restoration.rolling_ball. |
Calibrate a denoising function and return optimal J-invariant version. |
|
|
Cycle spinning (repeatedly apply func to shifted versions of x). |
Denoise image using bilateral filter. |
|
Perform non-local means denoising on 2D-4D grayscale or RGB images. |
|
Perform total variation denoising using split-Bregman optimization. |
|
Perform total variation denoising in nD. |
|
|
Perform wavelet denoising on an image. |
|
Create an ellipoid kernel for restoration.rolling_ball. |
|
Robust wavelet-based estimator of the (Gaussian) noise standard deviation. |
Inpaint masked points in image with biharmonic equations. |
|
|
Richardson-Lucy deconvolution. |
|
Estimate background intensity by rolling/translating a kernel. |
Unsupervised Wiener-Hunt deconvolution. |
|
|
Recover the original from a wrapped phase image. |
|
Wiener-Hunt deconvolution |
ball_kernel¶
- skimage.restoration.ball_kernel(radius, ndim)[source]¶
Create a ball kernel for restoration.rolling_ball.
- Parameters:
- radiusint
Radius of the ball.
- ndimint
Number of dimensions of the ball.
ndimshould match the dimensionality of the image the kernel will be applied to.
- Returns:
- kernelndarray
The kernel containing the surface intensity of the top half of the ellipsoid.
See also
calibrate_denoiser¶
- skimage.restoration.calibrate_denoiser(image, denoise_function, denoise_parameters, *, stride=4, approximate_loss=True, extra_output=False)[source]¶
Calibrate a denoising function and return optimal J-invariant version.
The returned function is partially evaluated with optimal parameter values set for denoising the input image.
- Parameters:
- imagendarray
Input data to be denoised (converted using img_as_float).
- denoise_functionfunction
Denoising function to be calibrated.
- denoise_parametersdict of list
Ranges of parameters for denoise_function to be calibrated over.
- strideint, optional
Stride used in masking procedure that converts denoise_function to J-invariance.
- approximate_lossbool, optional
Whether to approximate the self-supervised loss used to evaluate the denoiser by only computing it on one masked version of the image. If False, the runtime will be a factor of stride**image.ndim longer.
- extra_outputbool, optional
If True, return parameters and losses in addition to the calibrated denoising function
- Returns:
- best_denoise_functionfunction
The optimal J-invariant version of denoise_function.
- If extra_output is True, the following tuple is also returned:
- (parameters_tested, losses)tuple (list of dict, list of int)
List of parameters tested for denoise_function, as a dictionary of kwargs Self-supervised loss for each set of parameters in parameters_tested.
Notes
The calibration procedure uses a self-supervised mean-square-error loss to evaluate the performance of J-invariant versions of denoise_function. The minimizer of the self-supervised loss is also the minimizer of the ground-truth loss (i.e., the true MSE error) [1]. The returned function can be used on the original noisy image, or other images with similar characteristics.
- Increasing the stride increases the performance of best_denoise_function
at the expense of increasing its runtime. It has no effect on the runtime of the calibration.
References
[1]J. Batson & L. Royer. Noise2Self: Blind Denoising by Self-Supervision, International Conference on Machine Learning, p. 524-533 (2019).
Examples
>>> from skimage import color, data >>> from skimage.restoration import denoise_wavelet >>> import numpy as np >>> img = color.rgb2gray(data.astronaut()[:50, :50]) >>> rng = np.random.default_rng() >>> noisy = img + 0.5 * img.std() * rng.standard_normal(img.shape) >>> parameters = {'sigma': np.arange(0.1, 0.4, 0.02)} >>> denoising_function = calibrate_denoiser(noisy, denoise_wavelet, ... denoise_parameters=parameters) >>> denoised_img = denoising_function(img)
Examples using skimage.restoration.calibrate_denoiser¶

Full tutorial on calibrating Denoisers Using J-Invariance
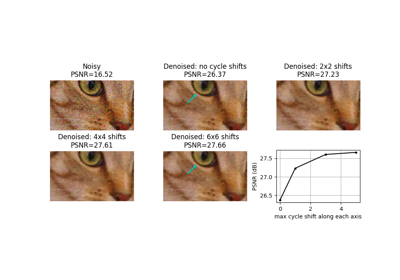
cycle_spin¶
- skimage.restoration.cycle_spin(x, func, max_shifts, shift_steps=1, num_workers=None, func_kw={}, *, channel_axis=None)[source]¶
Cycle spinning (repeatedly apply func to shifted versions of x).
- Parameters:
- xarray-like
Data for input to
func.- funcfunction
A function to apply to circularly shifted versions of
x. Should takexas its first argument. Any additional arguments can be supplied viafunc_kw.- max_shiftsint or tuple
If an integer, shifts in
range(0, max_shifts+1)will be used along each axis ofx. If a tuple,range(0, max_shifts[i]+1)will be along axis i.- shift_stepsint or tuple, optional
The step size for the shifts applied along axis, i, are::
range((0, max_shifts[i]+1, shift_steps[i])). If an integer is provided, the same step size is used for all axes.- num_workersint or None, optional
The number of parallel threads to use during cycle spinning. If set to
None, the full set of available cores are used.- func_kwdict, optional
Additional keyword arguments to supply to
func.- channel_axisint or None, optional
If None, the image is assumed to be a grayscale (single channel) image. Otherwise, this parameter indicates which axis of the array corresponds to channels.
New in version 0.19:
channel_axiswas added in 0.19.
- Returns:
- avg_ynp.ndarray
The output of
func(x, **func_kw)averaged over all combinations of the specified axis shifts.
Notes
Cycle spinning was proposed as a way to approach shift-invariance via performing several circular shifts of a shift-variant transform [1].
For a n-level discrete wavelet transforms, one may wish to perform all shifts up to
max_shifts = 2**n - 1. In practice, much of the benefit can often be realized with only a small number of shifts per axis.For transforms such as the blockwise discrete cosine transform, one may wish to evaluate shifts up to the block size used by the transform.
References
[1]R.R. Coifman and D.L. Donoho. “Translation-Invariant De-Noising”. Wavelets and Statistics, Lecture Notes in Statistics, vol.103. Springer, New York, 1995, pp.125-150. DOI:10.1007/978-1-4612-2544-7_9
Examples
>>> import skimage.data >>> from skimage import img_as_float >>> from skimage.restoration import denoise_wavelet, cycle_spin >>> img = img_as_float(skimage.data.camera()) >>> sigma = 0.1 >>> img = img + sigma * np.random.standard_normal(img.shape) >>> denoised = cycle_spin(img, func=denoise_wavelet, ... max_shifts=3)
Examples using skimage.restoration.cycle_spin¶
denoise_bilateral¶
- skimage.restoration.denoise_bilateral(image, win_size=None, sigma_color=None, sigma_spatial=1, bins=10000, mode='constant', cval=0, *, channel_axis=None)[source]¶
Denoise image using bilateral filter.
- Parameters:
- imagendarray, shape (M, N[, 3])
Input image, 2D grayscale or RGB.
- win_sizeint
Window size for filtering. If win_size is not specified, it is calculated as
max(5, 2 * ceil(3 * sigma_spatial) + 1).- sigma_colorfloat
Standard deviation for grayvalue/color distance (radiometric similarity). A larger value results in averaging of pixels with larger radiometric differences. If
None, the standard deviation ofimagewill be used.- sigma_spatialfloat
Standard deviation for range distance. A larger value results in averaging of pixels with larger spatial differences.
- binsint
Number of discrete values for Gaussian weights of color filtering. A larger value results in improved accuracy.
- mode{‘constant’, ‘edge’, ‘symmetric’, ‘reflect’, ‘wrap’}
How to handle values outside the image borders. See
numpy.padfor detail.- cvalstring
Used in conjunction with mode ‘constant’, the value outside the image boundaries.
- channel_axisint or None, optional
If
None, the image is assumed to be grayscale (single-channel). Otherwise, this parameter indicates which axis of the array corresponds to channels.New in version 0.19:
channel_axiswas added in 0.19.
- Returns:
- denoisedndarray
Denoised image.
Notes
This is an edge-preserving, denoising filter. It averages pixels based on their spatial closeness and radiometric similarity [1].
Spatial closeness is measured by the Gaussian function of the Euclidean distance between two pixels and a certain standard deviation (sigma_spatial).
Radiometric similarity is measured by the Gaussian function of the Euclidean distance between two color values and a certain standard deviation (sigma_color).
Note that, if the image is of any int dtype,
imagewill be converted using the img_as_float function and thus the standard deviation (sigma_color) will be in range[0, 1].For more information on scikit-image’s data type conversions and how images are rescaled in these conversions, see: https://scikit-image.org/docs/stable/user_guide/data_types.html.
References
[1]C. Tomasi and R. Manduchi. “Bilateral Filtering for Gray and Color Images.” IEEE International Conference on Computer Vision (1998) 839-846. DOI:10.1109/ICCV.1998.710815
Examples
>>> from skimage import data, img_as_float >>> astro = img_as_float(data.astronaut()) >>> astro = astro[220:300, 220:320] >>> rng = np.random.default_rng() >>> noisy = astro + 0.6 * astro.std() * rng.random(astro.shape) >>> noisy = np.clip(noisy, 0, 1) >>> denoised = denoise_bilateral(noisy, sigma_color=0.05, sigma_spatial=15, ... channel_axis=-1)
Examples using skimage.restoration.denoise_bilateral¶
denoise_nl_means¶
- skimage.restoration.denoise_nl_means(image, patch_size=7, patch_distance=11, h=0.1, fast_mode=True, sigma=0.0, *, preserve_range=False, channel_axis=None)[source]¶
Perform non-local means denoising on 2D-4D grayscale or RGB images.
- Parameters:
- image2D or 3D ndarray
Input image to be denoised, which can be 2D or 3D, and grayscale or RGB (for 2D images only, see
channel_axisparameter). There can be any number of channels (does not strictly have to be RGB).- patch_sizeint, optional
Size of patches used for denoising.
- patch_distanceint, optional
Maximal distance in pixels where to search patches used for denoising.
- hfloat, optional
Cut-off distance (in gray levels). The higher h, the more permissive one is in accepting patches. A higher h results in a smoother image, at the expense of blurring features. For a Gaussian noise of standard deviation sigma, a rule of thumb is to choose the value of h to be sigma of slightly less.
- fast_modebool, optional
If True (default value), a fast version of the non-local means algorithm is used. If False, the original version of non-local means is used. See the Notes section for more details about the algorithms.
- sigmafloat, optional
The standard deviation of the (Gaussian) noise. If provided, a more robust computation of patch weights is computed that takes the expected noise variance into account (see Notes below).
- preserve_rangebool, optional
Whether to keep the original range of values. Otherwise, the input image is converted according to the conventions of img_as_float. Also see https://scikit-image.org/docs/dev/user_guide/data_types.html
- channel_axisint or None, optional
If None, the image is assumed to be a grayscale (single channel) image. Otherwise, this parameter indicates which axis of the array corresponds to channels.
New in version 0.19:
channel_axiswas added in 0.19.
- Returns:
- resultndarray
Denoised image, of same shape as image.
Notes
The non-local means algorithm is well suited for denoising images with specific textures. The principle of the algorithm is to average the value of a given pixel with values of other pixels in a limited neighborhood, provided that the patches centered on the other pixels are similar enough to the patch centered on the pixel of interest.
In the original version of the algorithm [1], corresponding to
fast=False, the computational complexity is:image.size * patch_size ** image.ndim * patch_distance ** image.ndim
Hence, changing the size of patches or their maximal distance has a strong effect on computing times, especially for 3-D images.
However, the default behavior corresponds to
fast_mode=True, for which another version of non-local means [2] is used, corresponding to a complexity of:image.size * patch_distance ** image.ndim
The computing time depends only weakly on the patch size, thanks to the computation of the integral of patches distances for a given shift, that reduces the number of operations [1]. Therefore, this algorithm executes faster than the classic algorithm (
fast_mode=False), at the expense of using twice as much memory. This implementation has been proven to be more efficient compared to other alternatives, see e.g. [3].Compared to the classic algorithm, all pixels of a patch contribute to the distance to another patch with the same weight, no matter their distance to the center of the patch. This coarser computation of the distance can result in a slightly poorer denoising performance. Moreover, for small images (images with a linear size that is only a few times the patch size), the classic algorithm can be faster due to boundary effects.
The image is padded using the reflect mode of skimage.util.pad before denoising.
If the noise standard deviation, sigma, is provided a more robust computation of patch weights is used. Subtracting the known noise variance from the computed patch distances improves the estimates of patch similarity, giving a moderate improvement to denoising performance [4]. It was also mentioned as an option for the fast variant of the algorithm in [3].
When sigma is provided, a smaller h should typically be used to avoid oversmoothing. The optimal value for h depends on the image content and noise level, but a reasonable starting point is
h = 0.8 * sigmawhen fast_mode is True, orh = 0.6 * sigmawhen fast_mode is False.References
[1] (1,2)A. Buades, B. Coll, & J-M. Morel. A non-local algorithm for image denoising. In CVPR 2005, Vol. 2, pp. 60-65, IEEE. DOI:10.1109/CVPR.2005.38
[2]J. Darbon, A. Cunha, T.F. Chan, S. Osher, and G.J. Jensen, Fast nonlocal filtering applied to electron cryomicroscopy, in 5th IEEE International Symposium on Biomedical Imaging: From Nano to Macro, 2008, pp. 1331-1334. DOI:10.1109/ISBI.2008.4541250
[3] (1,2)Jacques Froment. Parameter-Free Fast Pixelwise Non-Local Means Denoising. Image Processing On Line, 2014, vol. 4, pp. 300-326. DOI:10.5201/ipol.2014.120
[4]A. Buades, B. Coll, & J-M. Morel. Non-Local Means Denoising. Image Processing On Line, 2011, vol. 1, pp. 208-212. DOI:10.5201/ipol.2011.bcm_nlm
Examples
>>> a = np.zeros((40, 40)) >>> a[10:-10, 10:-10] = 1. >>> rng = np.random.default_rng() >>> a += 0.3 * rng.standard_normal(a.shape) >>> denoised_a = denoise_nl_means(a, 7, 5, 0.1)
Examples using skimage.restoration.denoise_nl_means¶

Full tutorial on calibrating Denoisers Using J-Invariance
denoise_tv_bregman¶
- skimage.restoration.denoise_tv_bregman(image, weight=5.0, max_num_iter=100, eps=0.001, isotropic=True, *, channel_axis=None)[source]¶
Perform total variation denoising using split-Bregman optimization.
Given \(f\), a noisy image (input data), total variation denoising (also known as total variation regularization) aims to find an image \(u\) with less total variation than \(f\), under the constraint that \(u\) remain similar to \(f\). This can be expressed by the Rudin–Osher–Fatemi (ROF) minimization problem:
\[\min_{u} \sum_{i=0}^{N-1} \left( \left| \nabla{u_i} \right| + \frac{\lambda}{2}(f_i - u_i)^2 \right)\]where \(\lambda\) is a positive parameter. The first term of this cost function is the total variation; the second term represents data fidelity. As \(\lambda \to 0\), the total variation term dominates, forcing the solution to have smaller total variation, at the expense of looking less like the input data.
This code is an implementation of the split Bregman algorithm of Goldstein and Osher to solve the ROF problem ([1], [2], [3]).
- Parameters:
- imagendarray
Input image to be denoised (converted using
img_as_float()).- weightfloat, optional
Denoising weight. It is equal to \(\frac{\lambda}{2}\). Therefore, the smaller the weight, the more denoising (at the expense of less similarity to image).
- epsfloat, optional
Tolerance \(\varepsilon > 0\) for the stop criterion: The algorithm stops when \(\|u_n - u_{n-1}\|_2 < \varepsilon\).
- max_num_iterint, optional
Maximal number of iterations used for the optimization.
- isotropicboolean, optional
Switch between isotropic and anisotropic TV denoising.
- channel_axisint or None, optional
If
None, the image is assumed to be grayscale (single-channel). Otherwise, this parameter indicates which axis of the array corresponds to channels.New in version 0.19:
channel_axiswas added in 0.19.
- Returns:
- undarray
Denoised image.
See also
denoise_tv_chambollePerform total variation denoising in nD.
Notes
Ensure that channel_axis parameter is set appropriately for color images.
The principle of total variation denoising is explained in [4]. It is about minimizing the total variation of an image, which can be roughly described as the integral of the norm of the image gradient. Total variation denoising tends to produce cartoon-like images, that is, piecewise-constant images.
References
[1]Tom Goldstein and Stanley Osher, “The Split Bregman Method For L1 Regularized Problems”, https://ww3.math.ucla.edu/camreport/cam08-29.pdf
[2]Pascal Getreuer, “Rudin–Osher–Fatemi Total Variation Denoising using Split Bregman” in Image Processing On Line on 2012–05–19, https://www.ipol.im/pub/art/2012/g-tvd/article_lr.pdf
denoise_tv_chambolle¶
- skimage.restoration.denoise_tv_chambolle(image, weight=0.1, eps=0.0002, max_num_iter=200, *, channel_axis=None)[source]¶
Perform total variation denoising in nD.
Given \(f\), a noisy image (input data), total variation denoising (also known as total variation regularization) aims to find an image \(u\) with less total variation than \(f\), under the constraint that \(u\) remain similar to \(f\). This can be expressed by the Rudin–Osher–Fatemi (ROF) minimization problem:
\[\min_{u} \sum_{i=0}^{N-1} \left( \left| \nabla{u_i} \right| + \frac{\lambda}{2}(f_i - u_i)^2 \right)\]where \(\lambda\) is a positive parameter. The first term of this cost function is the total variation; the second term represents data fidelity. As \(\lambda \to 0\), the total variation term dominates, forcing the solution to have smaller total variation, at the expense of looking less like the input data.
This code is an implementation of the algorithm proposed by Chambolle in [1] to solve the ROF problem.
- Parameters:
- imagendarray
Input image to be denoised. If its dtype is not float, it gets converted with
img_as_float().- weightfloat, optional
Denoising weight. It is equal to \(\frac{1}{\lambda}\). Therefore, the greater the weight, the more denoising (at the expense of fidelity to image).
- epsfloat, optional
Tolerance \(\varepsilon > 0\) for the stop criterion (compares to absolute value of relative difference of the cost function \(E\)): The algorithm stops when \(|E_{n-1} - E_n| < \varepsilon * E_0\).
- max_num_iterint, optional
Maximal number of iterations used for the optimization.
- channel_axisint or None, optional
If
None, the image is assumed to be grayscale (single-channel). Otherwise, this parameter indicates which axis of the array corresponds to channels.New in version 0.19:
channel_axiswas added in 0.19.
- Returns:
- undarray
Denoised image.
See also
denoise_tv_bregmanPerform total variation denoising using split-Bregman optimization.
Notes
Make sure to set the channel_axis parameter appropriately for color images.
The principle of total variation denoising is explained in [2]. It is about minimizing the total variation of an image, which can be roughly described as the integral of the norm of the image gradient. Total variation denoising tends to produce cartoon-like images, that is, piecewise-constant images.
References
[1]A. Chambolle, An algorithm for total variation minimization and applications, Journal of Mathematical Imaging and Vision, Springer, 2004, 20, 89-97.
Examples
2D example on astronaut image:
>>> from skimage import color, data >>> img = color.rgb2gray(data.astronaut())[:50, :50] >>> rng = np.random.default_rng() >>> img += 0.5 * img.std() * rng.standard_normal(img.shape) >>> denoised_img = denoise_tv_chambolle(img, weight=60)
3D example on synthetic data:
>>> x, y, z = np.ogrid[0:20, 0:20, 0:20] >>> mask = (x - 22)**2 + (y - 20)**2 + (z - 17)**2 < 8**2 >>> mask = mask.astype(float) >>> rng = np.random.default_rng() >>> mask += 0.2 * rng.standard_normal(mask.shape) >>> res = denoise_tv_chambolle(mask, weight=100)
Examples using skimage.restoration.denoise_tv_chambolle¶

Full tutorial on calibrating Denoisers Using J-Invariance
denoise_wavelet¶
- skimage.restoration.denoise_wavelet(image, sigma=None, wavelet='db1', mode='soft', wavelet_levels=None, convert2ycbcr=False, method='BayesShrink', rescale_sigma=True, *, channel_axis=None)[source]¶
Perform wavelet denoising on an image.
- Parameters:
- imagendarray ([M[, N[, …P]][, C]) of ints, uints or floats
Input data to be denoised. image can be of any numeric type, but it is cast into an ndarray of floats for the computation of the denoised image.
- sigmafloat or list, optional
The noise standard deviation used when computing the wavelet detail coefficient threshold(s). When None (default), the noise standard deviation is estimated via the method in [2].
- waveletstring, optional
The type of wavelet to perform and can be any of the options
pywt.wavelistoutputs. The default is ‘db1’. For example,waveletcan be any of{'db2', 'haar', 'sym9'}and many more.- mode{‘soft’, ‘hard’}, optional
An optional argument to choose the type of denoising performed. It noted that choosing soft thresholding given additive noise finds the best approximation of the original image.
- wavelet_levelsint or None, optional
The number of wavelet decomposition levels to use. The default is three less than the maximum number of possible decomposition levels.
- convert2ycbcrbool, optional
If True and channel_axis is set, do the wavelet denoising in the YCbCr colorspace instead of the RGB color space. This typically results in better performance for RGB images.
- method{‘BayesShrink’, ‘VisuShrink’}, optional
Thresholding method to be used. The currently supported methods are “BayesShrink” [1] and “VisuShrink” [2]. Defaults to “BayesShrink”.
- rescale_sigmabool, optional
If False, no rescaling of the user-provided
sigmawill be performed. The default ofTruerescales sigma appropriately if the image is rescaled internally.New in version 0.16:
rescale_sigmawas introduced in 0.16- channel_axisint or None, optional
If
None, the image is assumed to be grayscale (single-channel). Otherwise, this parameter indicates which axis of the array corresponds to channels.New in version 0.19:
channel_axiswas added in 0.19.
- Returns:
- outndarray
Denoised image.
Notes
The wavelet domain is a sparse representation of the image, and can be thought of similarly to the frequency domain of the Fourier transform. Sparse representations have most values zero or near-zero and truly random noise is (usually) represented by many small values in the wavelet domain. Setting all values below some threshold to 0 reduces the noise in the image, but larger thresholds also decrease the detail present in the image.
If the input is 3D, this function performs wavelet denoising on each color plane separately.
Changed in version 0.16: For floating point inputs, the original input range is maintained and there is no clipping applied to the output. Other input types will be converted to a floating point value in the range [-1, 1] or [0, 1] depending on the input image range. Unless
rescale_sigma = False, any internal rescaling applied to theimagewill also be applied tosigmato maintain the same relative amplitude.Many wavelet coefficient thresholding approaches have been proposed. By default,
denoise_waveletapplies BayesShrink, which is an adaptive thresholding method that computes separate thresholds for each wavelet sub-band as described in [1].If
method == "VisuShrink", a single “universal threshold” is applied to all wavelet detail coefficients as described in [2]. This threshold is designed to remove all Gaussian noise at a givensigmawith high probability, but tends to produce images that appear overly smooth.Although any of the wavelets from
PyWaveletscan be selected, the thresholding methods assume an orthogonal wavelet transform and may not choose the threshold appropriately for biorthogonal wavelets. Orthogonal wavelets are desirable because white noise in the input remains white noise in the subbands. Biorthogonal wavelets lead to colored noise in the subbands. Additionally, the orthogonal wavelets in PyWavelets are orthonormal so that noise variance in the subbands remains identical to the noise variance of the input. Example orthogonal wavelets are the Daubechies (e.g. ‘db2’) or symmlet (e.g. ‘sym2’) families.References
[1] (1,2)Chang, S. Grace, Bin Yu, and Martin Vetterli. “Adaptive wavelet thresholding for image denoising and compression.” Image Processing, IEEE Transactions on 9.9 (2000): 1532-1546. DOI:10.1109/83.862633
[2] (1,2,3)D. L. Donoho and I. M. Johnstone. “Ideal spatial adaptation by wavelet shrinkage.” Biometrika 81.3 (1994): 425-455. DOI:10.1093/biomet/81.3.425
Examples
>>> from skimage import color, data >>> img = img_as_float(data.astronaut()) >>> img = color.rgb2gray(img) >>> rng = np.random.default_rng() >>> img += 0.1 * rng.standard_normal(img.shape) >>> img = np.clip(img, 0, 1) >>> denoised_img = denoise_wavelet(img, sigma=0.1, rescale_sigma=True)
Examples using skimage.restoration.denoise_wavelet¶

Full tutorial on calibrating Denoisers Using J-Invariance
ellipsoid_kernel¶
- skimage.restoration.ellipsoid_kernel(shape, intensity)[source]¶
Create an ellipoid kernel for restoration.rolling_ball.
- Parameters:
- shapearraylike
Length of the principal axis of the ellipsoid (excluding the intensity axis). The kernel needs to have the same dimensionality as the image it will be applied to.
- intensityint
Length of the intensity axis of the ellipsoid.
- Returns:
- kernelndarray
The kernel containing the surface intensity of the top half of the ellipsoid.
See also
Examples using skimage.restoration.ellipsoid_kernel¶

Use rolling-ball algorithm for estimating background intensity
estimate_sigma¶
- skimage.restoration.estimate_sigma(image, average_sigmas=False, *, channel_axis=None)[source]¶
Robust wavelet-based estimator of the (Gaussian) noise standard deviation.
- Parameters:
- imagendarray
Image for which to estimate the noise standard deviation.
- average_sigmasbool, optional
If true, average the channel estimates of sigma. Otherwise return a list of sigmas corresponding to each channel.
- channel_axisint or None, optional
If
None, the image is assumed to be grayscale (single-channel). Otherwise, this parameter indicates which axis of the array corresponds to channels.New in version 0.19:
channel_axiswas added in 0.19.
- Returns:
- sigmafloat or list
Estimated noise standard deviation(s). If multichannel is True and average_sigmas is False, a separate noise estimate for each channel is returned. Otherwise, the average of the individual channel estimates is returned.
Notes
This function assumes the noise follows a Gaussian distribution. The estimation algorithm is based on the median absolute deviation of the wavelet detail coefficients as described in section 4.2 of [1].
References
[1]D. L. Donoho and I. M. Johnstone. “Ideal spatial adaptation by wavelet shrinkage.” Biometrika 81.3 (1994): 425-455. DOI:10.1093/biomet/81.3.425
Examples
>>> import skimage.data >>> from skimage import img_as_float >>> img = img_as_float(skimage.data.camera()) >>> sigma = 0.1 >>> rng = np.random.default_rng() >>> img = img + sigma * rng.standard_normal(img.shape) >>> sigma_hat = estimate_sigma(img, channel_axis=None)
Examples using skimage.restoration.estimate_sigma¶

Full tutorial on calibrating Denoisers Using J-Invariance
inpaint_biharmonic¶
- skimage.restoration.inpaint_biharmonic(image, mask, *, split_into_regions=False, channel_axis=None)[source]¶
Inpaint masked points in image with biharmonic equations.
- Parameters:
- image(M[, N[, …, P]][, C]) ndarray
Input image.
- mask(M[, N[, …, P]]) ndarray
Array of pixels to be inpainted. Have to be the same shape as one of the ‘image’ channels. Unknown pixels have to be represented with 1, known pixels - with 0.
- split_into_regionsboolean, optional
If True, inpainting is performed on a region-by-region basis. This is likely to be slower, but will have reduced memory requirements.
- channel_axisint or None, optional
If None, the image is assumed to be a grayscale (single channel) image. Otherwise, this parameter indicates which axis of the array corresponds to channels.
New in version 0.19:
channel_axiswas added in 0.19.
- Returns:
- out(M[, N[, …, P]][, C]) ndarray
Input image with masked pixels inpainted.
References
[1]S.B.Damelin and N.S.Hoang. “On Surface Completion and Image Inpainting by Biharmonic Functions: Numerical Aspects”, International Journal of Mathematics and Mathematical Sciences, Vol. 2018, Article ID 3950312 DOI:10.1155/2018/3950312
[2]C. K. Chui and H. N. Mhaskar, MRA Contextual-Recovery Extension of Smooth Functions on Manifolds, Appl. and Comp. Harmonic Anal., 28 (2010), 104-113, DOI:10.1016/j.acha.2009.04.004
Examples
>>> img = np.tile(np.square(np.linspace(0, 1, 5)), (5, 1)) >>> mask = np.zeros_like(img) >>> mask[2, 2:] = 1 >>> mask[1, 3:] = 1 >>> mask[0, 4:] = 1 >>> out = inpaint_biharmonic(img, mask)
Examples using skimage.restoration.inpaint_biharmonic¶
richardson_lucy¶
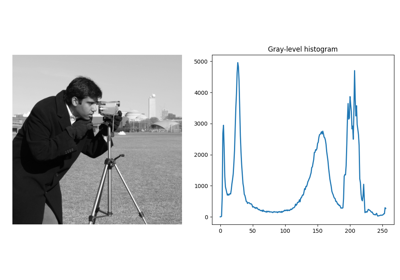
- skimage.restoration.richardson_lucy(image, psf, num_iter=50, clip=True, filter_epsilon=None)[source]¶
Richardson-Lucy deconvolution.
- Parameters:
- imagendarray
Input degraded image (can be n-dimensional).
- psfndarray
The point spread function.
- num_iterint, optional
Number of iterations. This parameter plays the role of regularisation.
- clipboolean, optional
True by default. If true, pixel value of the result above 1 or under -1 are thresholded for skimage pipeline compatibility.
- filter_epsilon: float, optional
Value below which intermediate results become 0 to avoid division by small numbers.
- Returns:
- im_deconvndarray
The deconvolved image.
References
Examples
>>> from skimage import img_as_float, data, restoration >>> camera = img_as_float(data.camera()) >>> from scipy.signal import convolve2d >>> psf = np.ones((5, 5)) / 25 >>> camera = convolve2d(camera, psf, 'same') >>> rng = np.random.default_rng() >>> camera += 0.1 * camera.std() * rng.standard_normal(camera.shape) >>> deconvolved = restoration.richardson_lucy(camera, psf, 5)
Examples using skimage.restoration.richardson_lucy¶
rolling_ball¶
- skimage.restoration.rolling_ball(image, *, radius=100, kernel=None, nansafe=False, num_threads=None)[source]¶
Estimate background intensity by rolling/translating a kernel.
This rolling ball algorithm estimates background intensity for a ndimage in case of uneven exposure. It is a generalization of the frequently used rolling ball algorithm [1].
- Parameters:
- imagendarray
The image to be filtered.
- radiusint, optional
Radius of a ball shaped kernel to be rolled/translated in the image. Used if
kernel = None.- kernelndarray, optional
The kernel to be rolled/translated in the image. It must have the same number of dimensions as
image. Kernel is filled with the intensity of the kernel at that position.- nansafe: bool, optional
If
False(default) assumes that none of the values inimagearenp.nan, and uses a faster implementation.- num_threads: int, optional
The maximum number of threads to use. If
Noneuse the OpenMP default value; typically equal to the maximum number of virtual cores. Note: This is an upper limit to the number of threads. The exact number is determined by the system’s OpenMP library.
- Returns:
- backgroundndarray
The estimated background of the image.
Notes
For the pixel that has its background intensity estimated (without loss of generality at
center) the rolling ball method centerskernelunder it and raises the kernel until the surface touches the image umbra at somepos=(y,x). The background intensity is then estimated using the image intensity at that position (image[pos]) plus the difference ofkernel[center] - kernel[pos].This algorithm assumes that dark pixels correspond to the background. If you have a bright background, invert the image before passing it to the function, e.g., using utils.invert. See the gallery example for details.
This algorithm is sensitive to noise (in particular salt-and-pepper noise). If this is a problem in your image, you can apply mild gaussian smoothing before passing the image to this function.
References
[1]Sternberg, Stanley R. “Biomedical image processing.” Computer 1 (1983): 22-34. DOI:10.1109/MC.1983.1654163
Examples
>>> import numpy as np >>> from skimage import data >>> from skimage.restoration import rolling_ball >>> image = data.coins() >>> background = rolling_ball(data.coins()) >>> filtered_image = image - background
>>> import numpy as np >>> from skimage import data >>> from skimage.restoration import rolling_ball, ellipsoid_kernel >>> image = data.coins() >>> kernel = ellipsoid_kernel((101, 101), 75) >>> background = rolling_ball(data.coins(), kernel=kernel) >>> filtered_image = image - background
Examples using skimage.restoration.rolling_ball¶

Use rolling-ball algorithm for estimating background intensity
unsupervised_wiener¶
- skimage.restoration.unsupervised_wiener(image, psf, reg=None, user_params=None, is_real=True, clip=True, *, random_state=None)[source]¶
Unsupervised Wiener-Hunt deconvolution.
Return the deconvolution with a Wiener-Hunt approach, where the hyperparameters are automatically estimated. The algorithm is a stochastic iterative process (Gibbs sampler) described in the reference below. See also
wienerfunction.- Parameters:
- image(M, N) ndarray
The input degraded image.
- psfndarray
The impulse response (input image’s space) or the transfer function (Fourier space). Both are accepted. The transfer function is automatically recognized as being complex (
np.iscomplexobj(psf)).- regndarray, optional
The regularisation operator. The Laplacian by default. It can be an impulse response or a transfer function, as for the psf.
- user_paramsdict, optional
Dictionary of parameters for the Gibbs sampler. See below.
- clipboolean, optional
True by default. If true, pixel values of the result above 1 or under -1 are thresholded for skimage pipeline compatibility.
- random_state{None, int,
numpy.random.Generator}, optional If random_state is None the
numpy.random.Generatorsingleton is used. If random_state is an int, a newGeneratorinstance is used, seeded with random_state. If random_state is already aGeneratorinstance then that instance is used.New in version 0.19.
- Returns:
- x_postmean(M, N) ndarray
The deconvolved image (the posterior mean).
- chainsdict
The keys
noiseandpriorcontain the chain list of noise and prior precision respectively.
- Other Parameters:
- The keys of ``user_params`` are:
- thresholdfloat
The stopping criterion: the norm of the difference between to successive approximated solution (empirical mean of object samples, see Notes section). 1e-4 by default.
- burninint
The number of sample to ignore to start computation of the mean. 15 by default.
- min_num_iterint
The minimum number of iterations. 30 by default.
- max_num_iterint
The maximum number of iterations if
thresholdis not satisfied. 200 by default.- callbackcallable (None by default)
A user provided callable to which is passed, if the function exists, the current image sample for whatever purpose. The user can store the sample, or compute other moments than the mean. It has no influence on the algorithm execution and is only for inspection.
Notes
The estimated image is design as the posterior mean of a probability law (from a Bayesian analysis). The mean is defined as a sum over all the possible images weighted by their respective probability. Given the size of the problem, the exact sum is not tractable. This algorithm use of MCMC to draw image under the posterior law. The practical idea is to only draw highly probable images since they have the biggest contribution to the mean. At the opposite, the less probable images are drawn less often since their contribution is low. Finally, the empirical mean of these samples give us an estimation of the mean, and an exact computation with an infinite sample set.
References
[1]François Orieux, Jean-François Giovannelli, and Thomas Rodet, “Bayesian estimation of regularization and point spread function parameters for Wiener-Hunt deconvolution”, J. Opt. Soc. Am. A 27, 1593-1607 (2010)
https://www.osapublishing.org/josaa/abstract.cfm?URI=josaa-27-7-1593
Examples
>>> from skimage import color, data, restoration >>> img = color.rgb2gray(data.astronaut()) >>> from scipy.signal import convolve2d >>> psf = np.ones((5, 5)) / 25 >>> img = convolve2d(img, psf, 'same') >>> rng = np.random.default_rng() >>> img += 0.1 * img.std() * rng.standard_normal(img.shape) >>> deconvolved_img = restoration.unsupervised_wiener(img, psf)
Examples using skimage.restoration.unsupervised_wiener¶
unwrap_phase¶
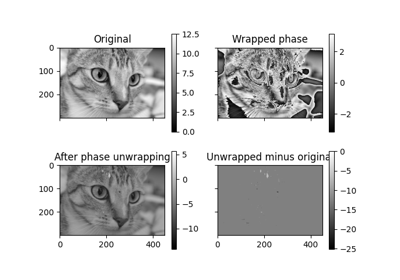
- skimage.restoration.unwrap_phase(image, wrap_around=False, seed=None)[source]¶
Recover the original from a wrapped phase image.
From an image wrapped to lie in the interval [-pi, pi), recover the original, unwrapped image.
- Parameters:
- image1D, 2D or 3D ndarray of floats, optionally a masked array
The values should be in the range [-pi, pi). If a masked array is provided, the masked entries will not be changed, and their values will not be used to guide the unwrapping of neighboring, unmasked values. Masked 1D arrays are not allowed, and will raise a ValueError.
- wrap_aroundbool or sequence of bool, optional
When an element of the sequence is True, the unwrapping process will regard the edges along the corresponding axis of the image to be connected and use this connectivity to guide the phase unwrapping process. If only a single boolean is given, it will apply to all axes. Wrap around is not supported for 1D arrays.
- seedint, optional
Unwrapping 2D or 3D images uses random initialization. This sets the seed of the PRNG to achieve deterministic behavior.
- Returns:
- image_unwrappedarray_like, double
Unwrapped image of the same shape as the input. If the input image was a masked array, the mask will be preserved.
- Raises:
- ValueError
If called with a masked 1D array or called with a 1D array and
wrap_around=True.
References
[1]Miguel Arevallilo Herraez, David R. Burton, Michael J. Lalor, and Munther A. Gdeisat, “Fast two-dimensional phase-unwrapping algorithm based on sorting by reliability following a noncontinuous path”, Journal Applied Optics, Vol. 41, No. 35 (2002) 7437,
[2]Abdul-Rahman, H., Gdeisat, M., Burton, D., & Lalor, M., “Fast three-dimensional phase-unwrapping algorithm based on sorting by reliability following a non-continuous path. In W. Osten, C. Gorecki, & E. L. Novak (Eds.), Optical Metrology (2005) 32–40, International Society for Optics and Photonics.
Examples
>>> c0, c1 = np.ogrid[-1:1:128j, -1:1:128j] >>> image = 12 * np.pi * np.exp(-(c0**2 + c1**2)) >>> image_wrapped = np.angle(np.exp(1j * image)) >>> image_unwrapped = unwrap_phase(image_wrapped) >>> np.std(image_unwrapped - image) < 1e-6 # A constant offset is normal True
Examples using skimage.restoration.unwrap_phase¶
wiener¶
- skimage.restoration.wiener(image, psf, balance, reg=None, is_real=True, clip=True)[source]¶
Wiener-Hunt deconvolution
Return the deconvolution with a Wiener-Hunt approach (i.e. with Fourier diagonalisation).
- Parameters:
- imagendarray
Input degraded image (can be n-dimensional).
- psfndarray
Point Spread Function. This is assumed to be the impulse response (input image space) if the data-type is real, or the transfer function (Fourier space) if the data-type is complex. There is no constraints on the shape of the impulse response. The transfer function must be of shape (N1, N2, …, ND) if is_real is True, (N1, N2, …, ND // 2 + 1) otherwise (see np.fft.rfftn).
- balancefloat
The regularisation parameter value that tunes the balance between the data adequacy that improve frequency restoration and the prior adequacy that reduce frequency restoration (to avoid noise artifacts).
- regndarray, optional
The regularisation operator. The Laplacian by default. It can be an impulse response or a transfer function, as for the psf. Shape constraint is the same as for the psf parameter.
- is_realboolean, optional
True by default. Specify if
psfandregare provided with hermitian hypothesis, that is only half of the frequency plane is provided (due to the redundancy of Fourier transform of real signal). It’s apply only ifpsfand/orregare provided as transfer function. For the hermitian property seeuftmodule ornp.fft.rfftn.- clipboolean, optional
True by default. If True, pixel values of the result above 1 or under -1 are thresholded for skimage pipeline compatibility.
- Returns:
- im_deconv(M, N) ndarray
The deconvolved image.
Notes
This function applies the Wiener filter to a noisy and degraded image by an impulse response (or PSF). If the data model is
\[y = Hx + n\]where \(n\) is noise, \(H\) the PSF and \(x\) the unknown original image, the Wiener filter is
\[\hat x = F^\dagger (|\Lambda_H|^2 + \lambda |\Lambda_D|^2) \Lambda_H^\dagger F y\]where \(F\) and \(F^\dagger\) are the Fourier and inverse Fourier transforms respectively, \(\Lambda_H\) the transfer function (or the Fourier transform of the PSF, see [Hunt] below) and \(\Lambda_D\) the filter to penalize the restored image frequencies (Laplacian by default, that is penalization of high frequency). The parameter \(\lambda\) tunes the balance between the data (that tends to increase high frequency, even those coming from noise), and the regularization.
These methods are then specific to a prior model. Consequently, the application or the true image nature must correspond to the prior model. By default, the prior model (Laplacian) introduce image smoothness or pixel correlation. It can also be interpreted as high-frequency penalization to compensate the instability of the solution with respect to the data (sometimes called noise amplification or “explosive” solution).
Finally, the use of Fourier space implies a circulant property of \(H\), see [2].
References
[1]François Orieux, Jean-François Giovannelli, and Thomas Rodet, “Bayesian estimation of regularization and point spread function parameters for Wiener-Hunt deconvolution”, J. Opt. Soc. Am. A 27, 1593-1607 (2010)
https://www.osapublishing.org/josaa/abstract.cfm?URI=josaa-27-7-1593
[2]B. R. Hunt “A matrix theory proof of the discrete convolution theorem”, IEEE Trans. on Audio and Electroacoustics, vol. au-19, no. 4, pp. 285-288, dec. 1971
Examples
>>> from skimage import color, data, restoration >>> img = color.rgb2gray(data.astronaut()) >>> from scipy.signal import convolve2d >>> psf = np.ones((5, 5)) / 25 >>> img = convolve2d(img, psf, 'same') >>> rng = np.random.default_rng() >>> img += 0.1 * img.std() * rng.standard_normal(img.shape) >>> deconvolved_img = restoration.wiener(img, psf, 0.1)

 Source
Source